On the Error Exponent of the Two-way Gaussian Channel
Sponsors:
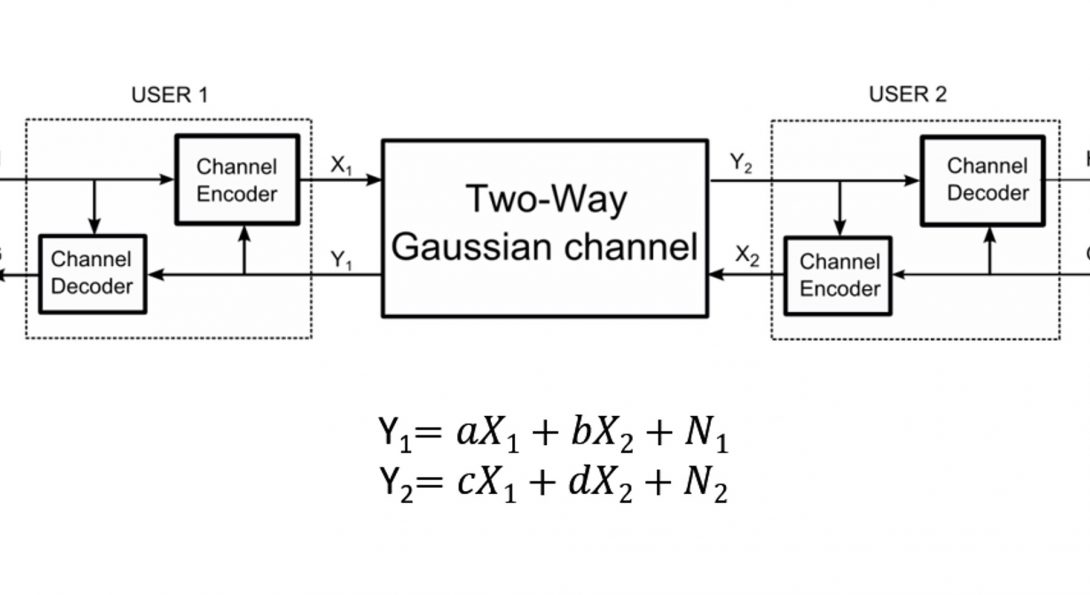
Problem Statement and Motivation
- Shannon introduced the Gaussian Channel in 1948.
- Channel coding theorem states that for any rate R below the channel capacity C, the probability of error can be made arbitrarily small Ρ_e → 0, as the block length n goes to infinity n → ∞.
- Infinite block lengths are not practical, therefore, the exponential decay of error probability needs to be studied.
- The reliability function of the one-way Gaussian channel is already known for AWGN communication schemes with and without feedback but it is not for the TWGC.
Technical Approach
- Reliability function example:
Key Achievements and Future Goals
- As work is still in progress we present some future goals:
- Error exponent results of a single bit transmission over a one-way Gaussian channel with feedback may be used to study the error exponent of the two-way Gaussian channel.
- For TWGC, we expect to characterize the trade off between error exponents in the two communication directions.
